Complex rectangles 2

I want to return to yesterday's problem from Visual Complex Analysis.

Suppose we have four complex numbers \(A, B, C, D\) on the unit circle such that \(A + B + C + D = 0\). We want to show that these points must form a rectangle. How can we do this?

An intuition I had last time was that we might want to draw the vector-loop picture of these points. Let's do that now.

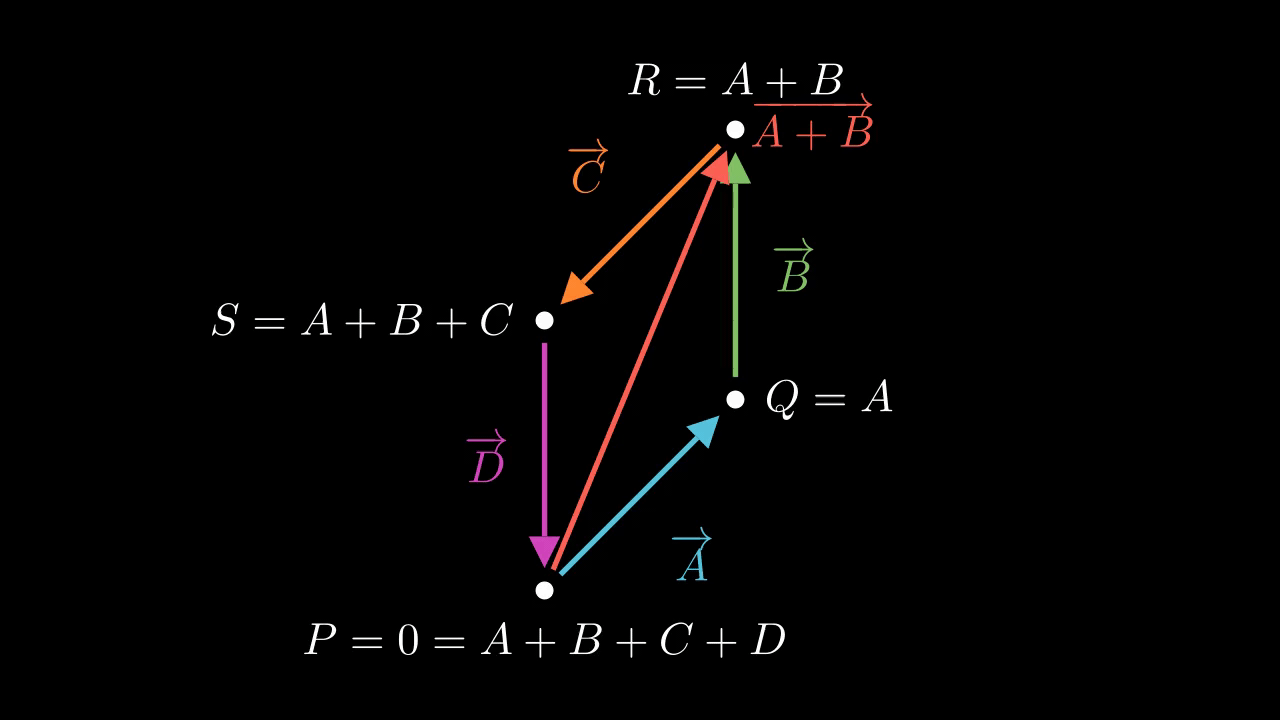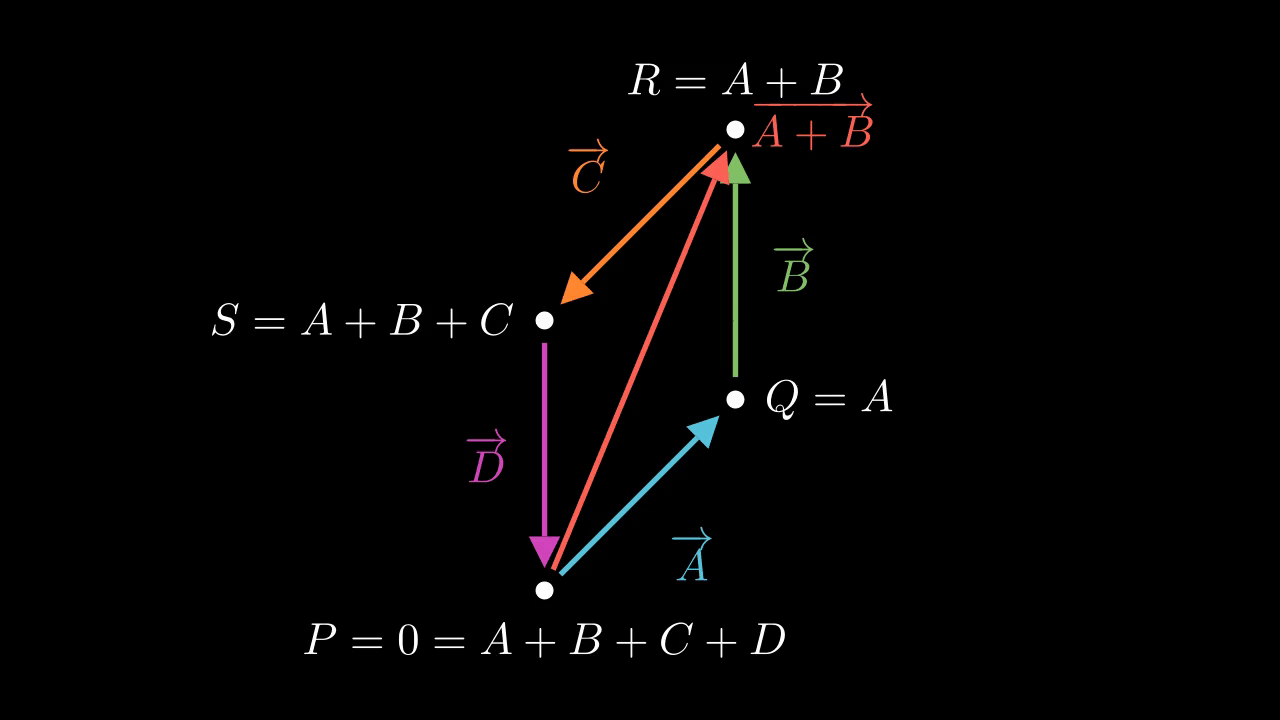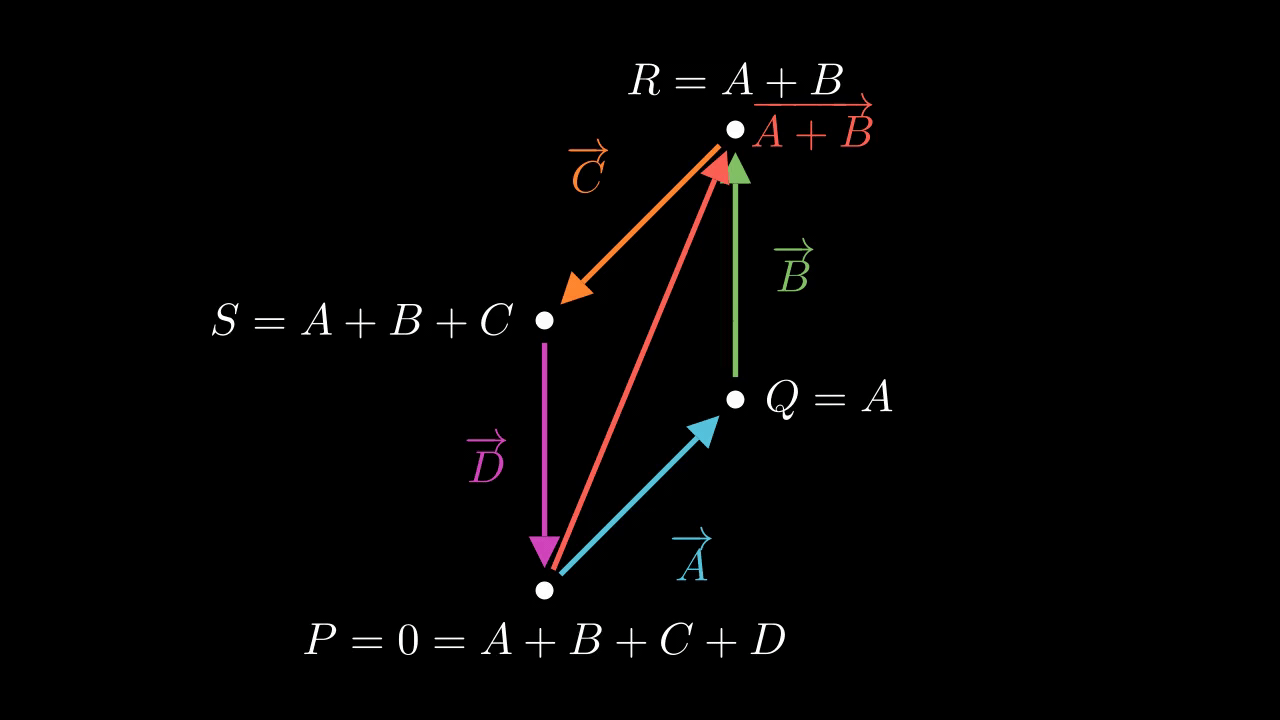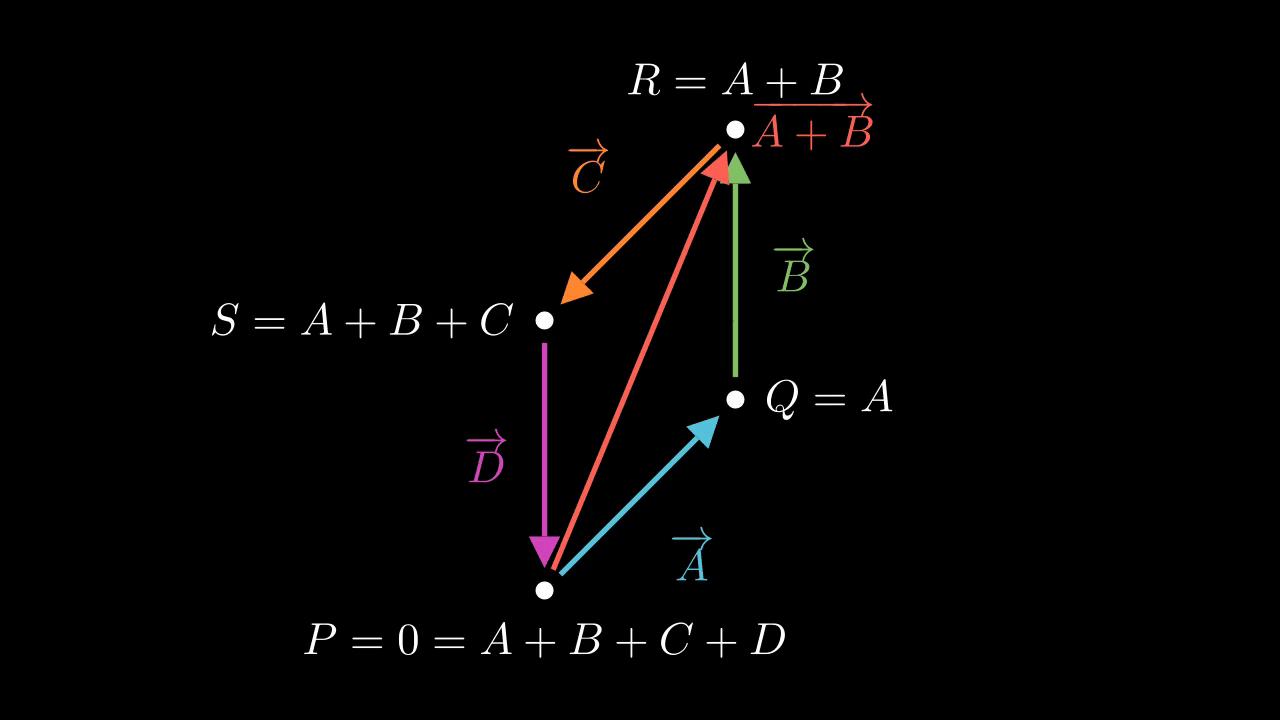
Figure 1 shows the situation. Here, \(P = 0, Q = A, R = A + B\), and \(S = A+B+C\). We draw each complex number as a vector joining this four points, and we also draw the diameter \(A + B\) connecting \(P\) with \(R\).

The key idea here is to relate these as two isoceles triangles, which forces the angles to be equal. Because \(A, B, C\), and \(D\) lie on the unit circle, they are all equal in magnitude, so that the outer sides are all equal. But the diameter \(A + B\) is common, so the triangles \(PQR\) and \(PSR\) are side-side-side congruent. This means the corresponding angles must be equal. The angle of \(A\) with \(B\) and the angle of \(C\) with \(D\) are equal, to start with. But because these are isoceles triangles, the base angles are equal to each other, so the angles of \(B\) with \(C\) and the angle of \(A\) with \(D\) are equal. This is true of the end-to-end angles, but also the base-to-base angles because the base-to-base angles are the corresponding complementary angles. So, the angles work out equal.

In fact, we can go further: The angle between \(A\) and \(B\) is complementary with that between \(B\) and \(C\). We know this because the two base angles of each isocoles triangle taken together must be complementary to the third. Here, the third angles are \(\angle PQR\) and \(\angle PSR\), also known as the angles between \(A\) and \(B\) and between \(C\) and \(D\). But the two base angles together are equal to the angle between\(B\) and \(C\), or equivalently between \(A\) and \(D\). So, the angle between \(A\) and \(B\) is complementary with that between \(C\) and \(D\). For the same reason the angle between \(C\) and \(D\) is complementary with the angle between \(D\) and \(A\). So, the angles work out as complementary.

This shows almost exactly what we want. Clearly, the angles being complementary means we should have \(A = -C\) and \(B = -D\). That in turn implies that \(A + B = -C - D\) hence \(|A + C| = |C + D|\) so that the four points \(A, B, C, D\) form a rectangle.

But this connection between the geometry and the complex numbers is a little tenuous for my taste. I would like to spell it out in more detail. This seems tricky. Can we relate the geometry back to statements about complex numbers?

Actually, I think we can. I think we can restate the complementary angles claim as saying that the products of certain complex numbers must be -1, the complex number with angle \(\pi\). That's because complex numbers adds their angles. The question is what complex number expresses the right angles. I think the answer is \((B/A)(C/B)\). Inverting a complex number negates the angle, and we're interested in the angles between complex numbers.

Let's make this a bit more formal. Say that we write \(A, B, C, D\) as \(e^{i \alpha}, e^{i \beta}, e^{i \gamma}, e^{i \delta}\) where \(0 \leq \alpha < \beta < \gamma < \delta < 2\pi \). I think we can state the complementary angles  Saying that the angle between \(A\) and \(B\) are complementary with the angle between \(B\) and \(C\) is equivalent to saying that \((\beta - \alpha) + (\gamma - \beta) = \gamma - \alpha = \pi\). But \(B/A = e^{i (\beta - \alpha)}\) and similarly for the other configurations. So as statements about complex numbers this is equivalent to saying \((B/A)(C/B) = C/A = -1\), or \(A = -C\).

But we've already proven this. The geometric approach we've just taken shows exactly that \((\beta - \alpha) + (\gamma - \beta) = \pi\) as desired.

This feels a little disorienting. It feels like I'm still missing a step. I think I'm missing the step where we explicitly relate the angles in the diagram to the complex numbers \(A, B, C\), and \(D\).

I think we need another diagram.

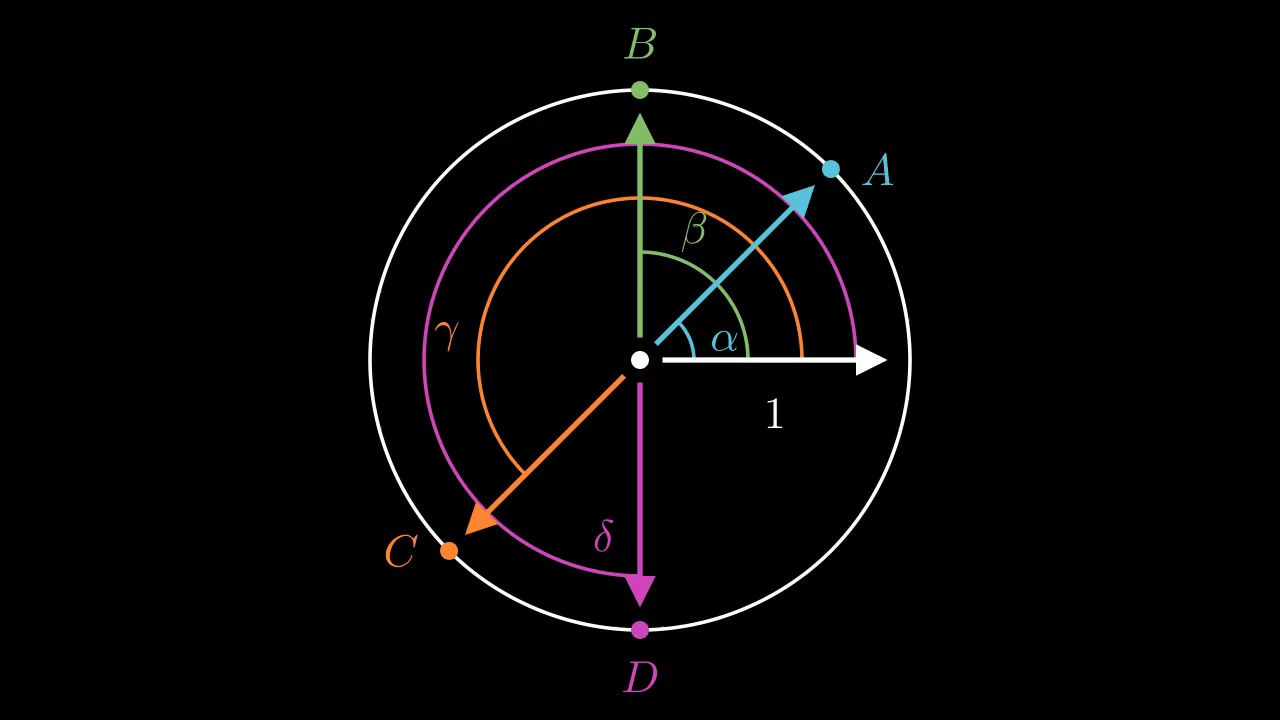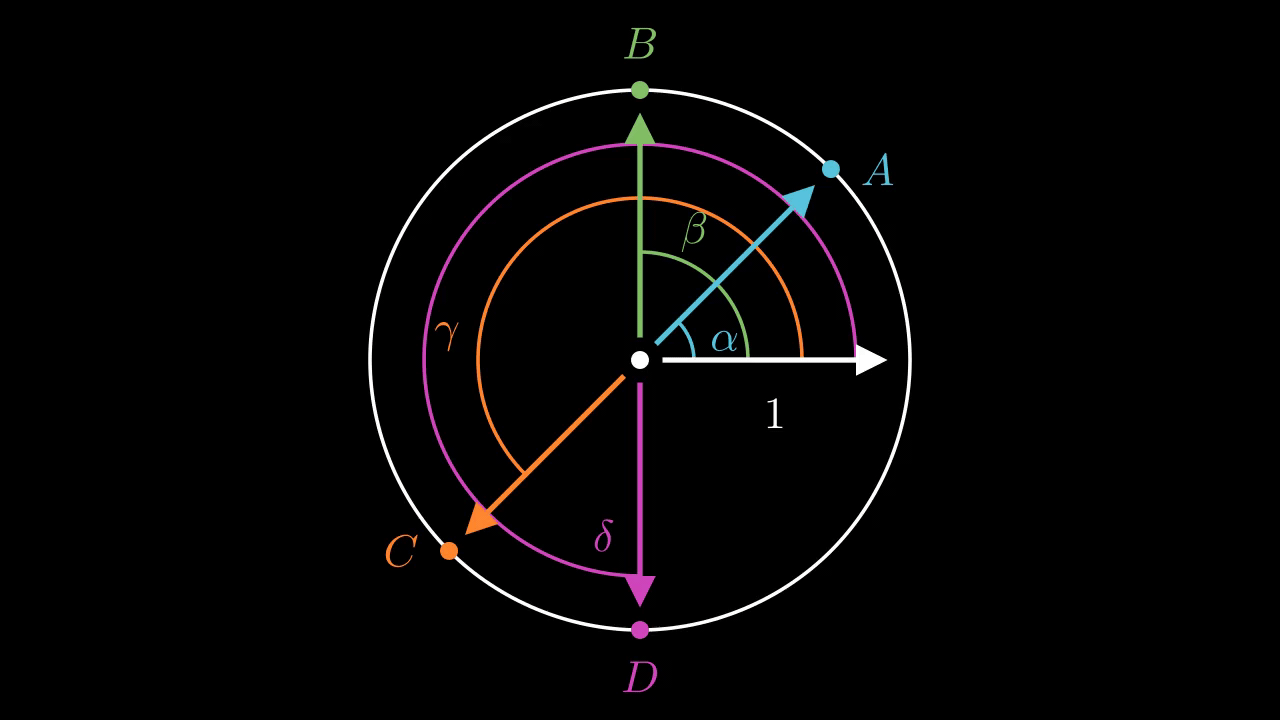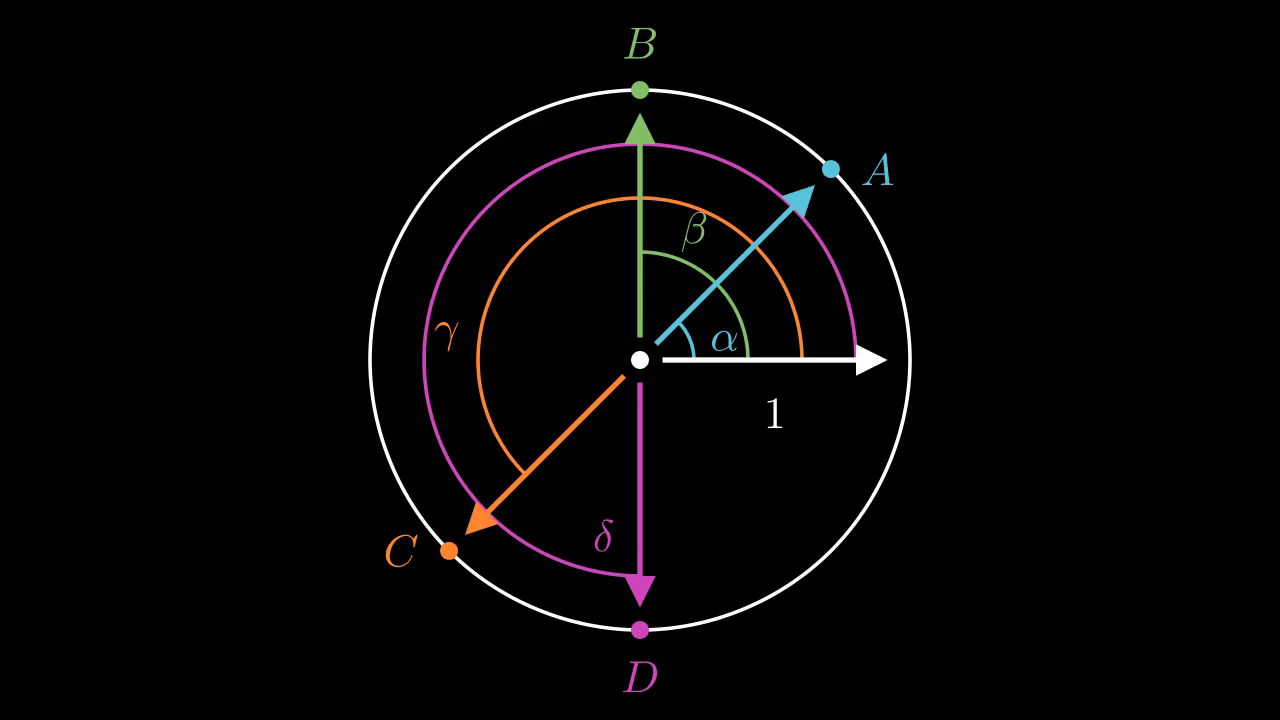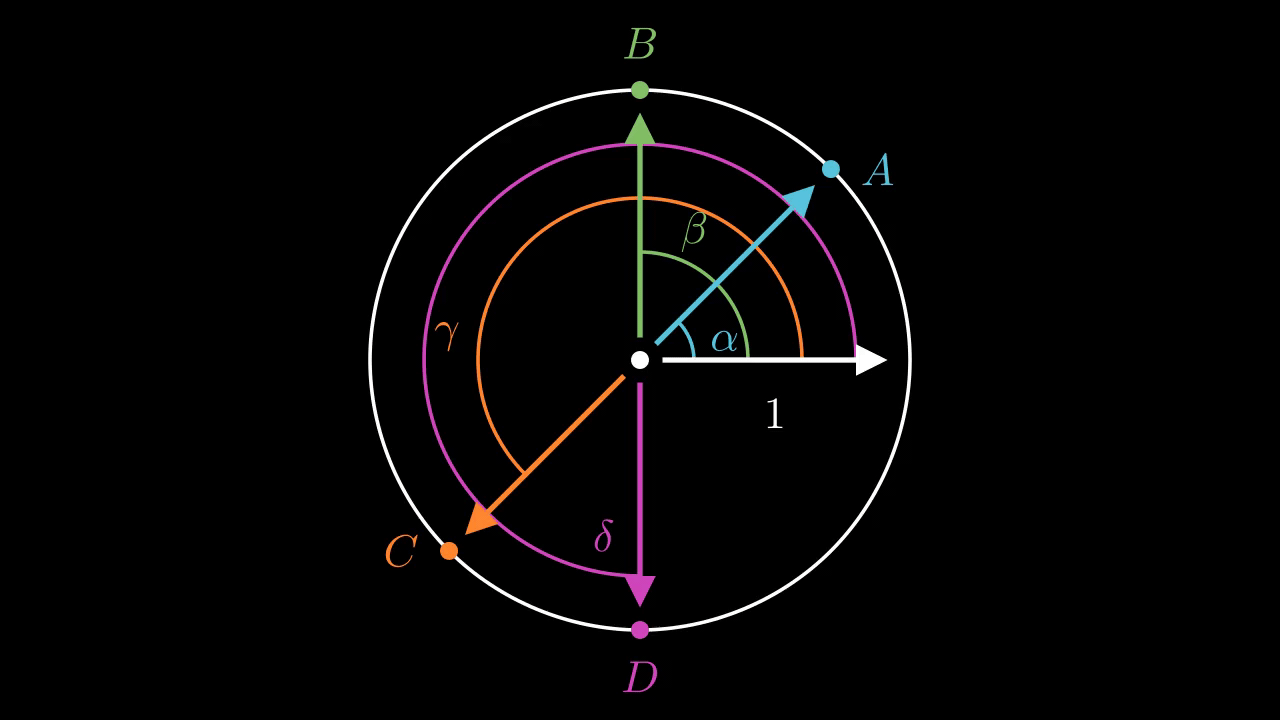
This pretty clearly shows that the relationship just described should hold.

Can we make this same kind of argument algrebraically? Tune in next time.