Complex rectangles 3

Last time we made a geometric argument that given four complex numbers \(A, B, C, D\) lying on the unit circle, if they satisfy \(A + B + C + D = 0\), then they form a rectangle.

Okay, technically, I didn't show the rectangle part. I did show the segments are opposite. It's pretty straightforward to see then that we have two lines of equal length crossing at their midpoints, so the endpoints should form a rectangle. We can form the rectangle out of four isoceles triangles, and opposite triangles must be similar to each other by side-angle-side congruence.

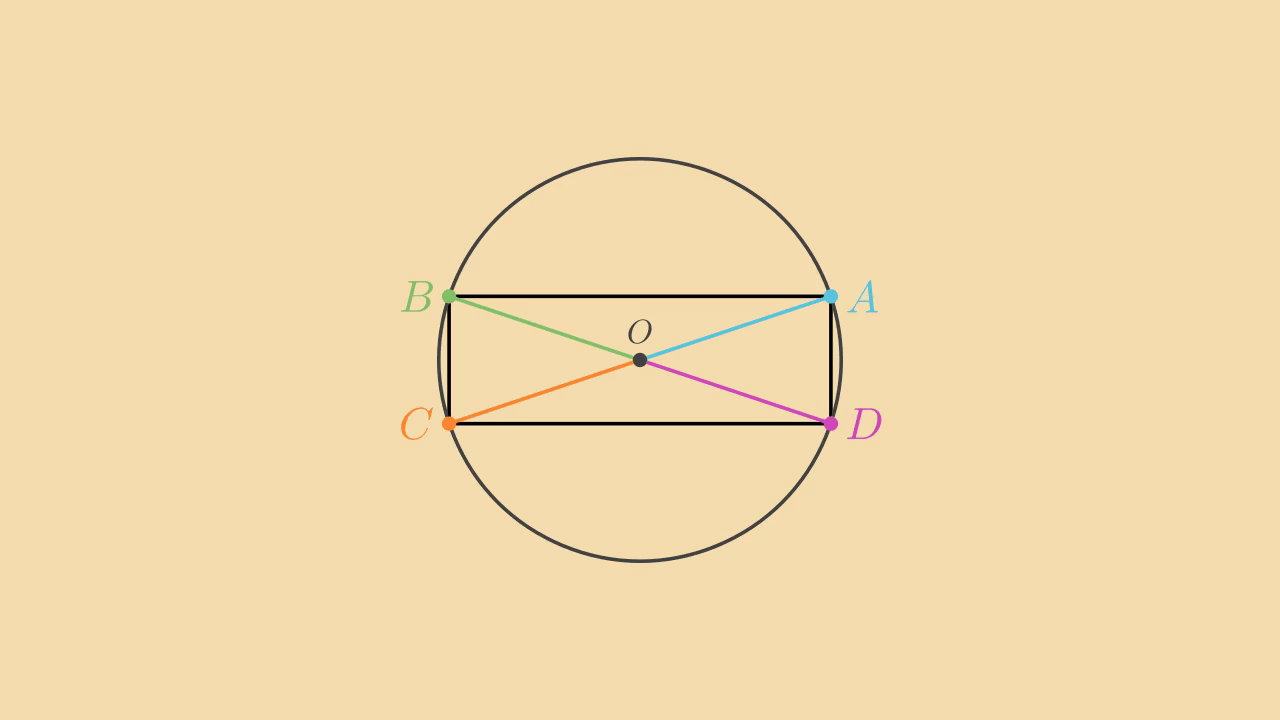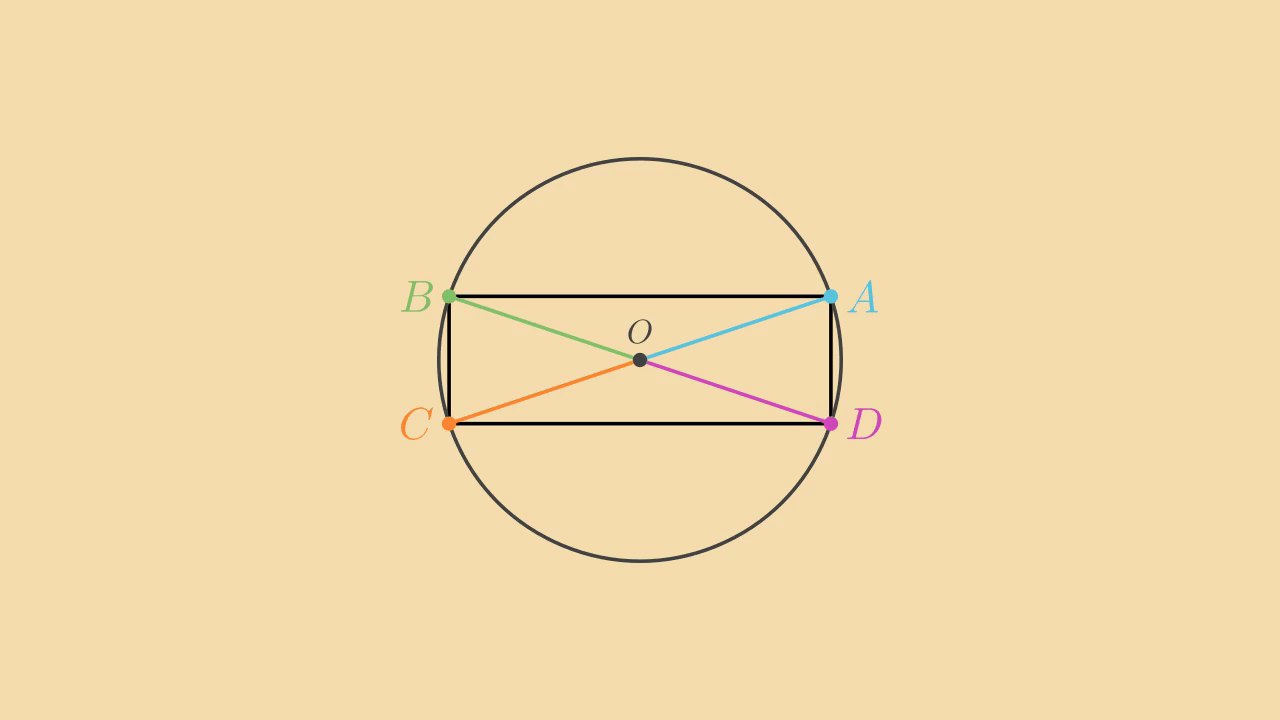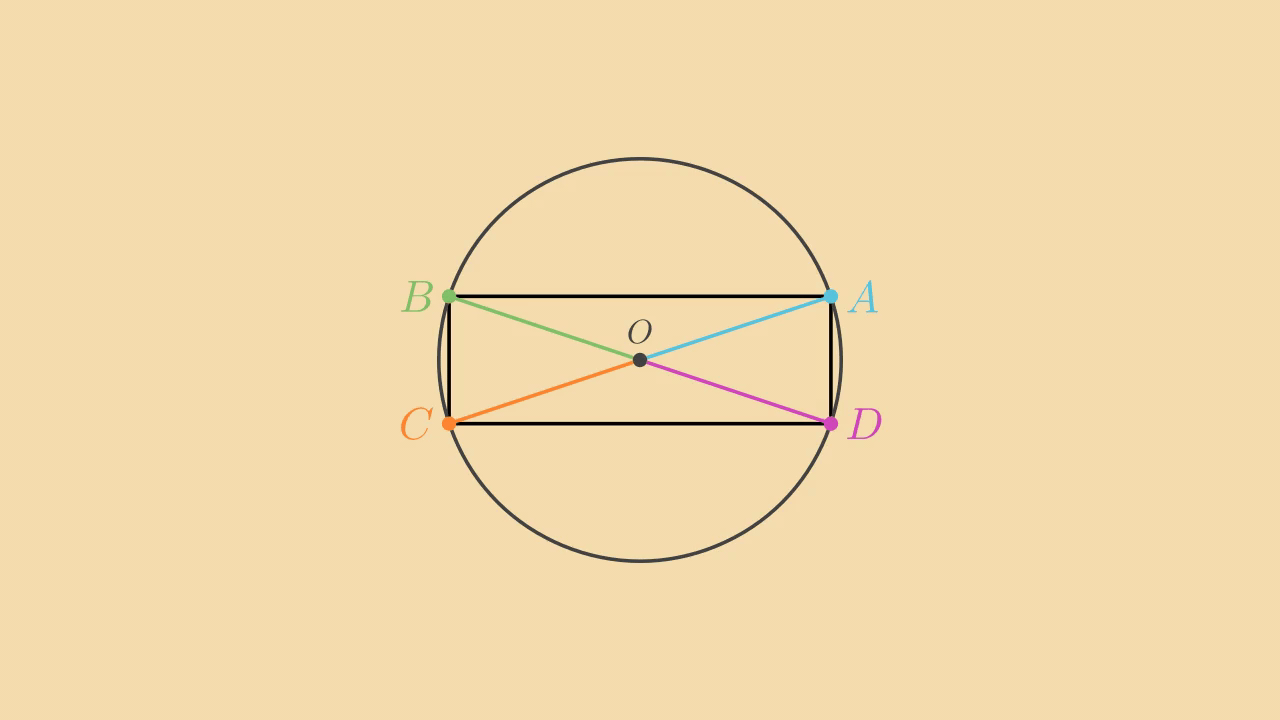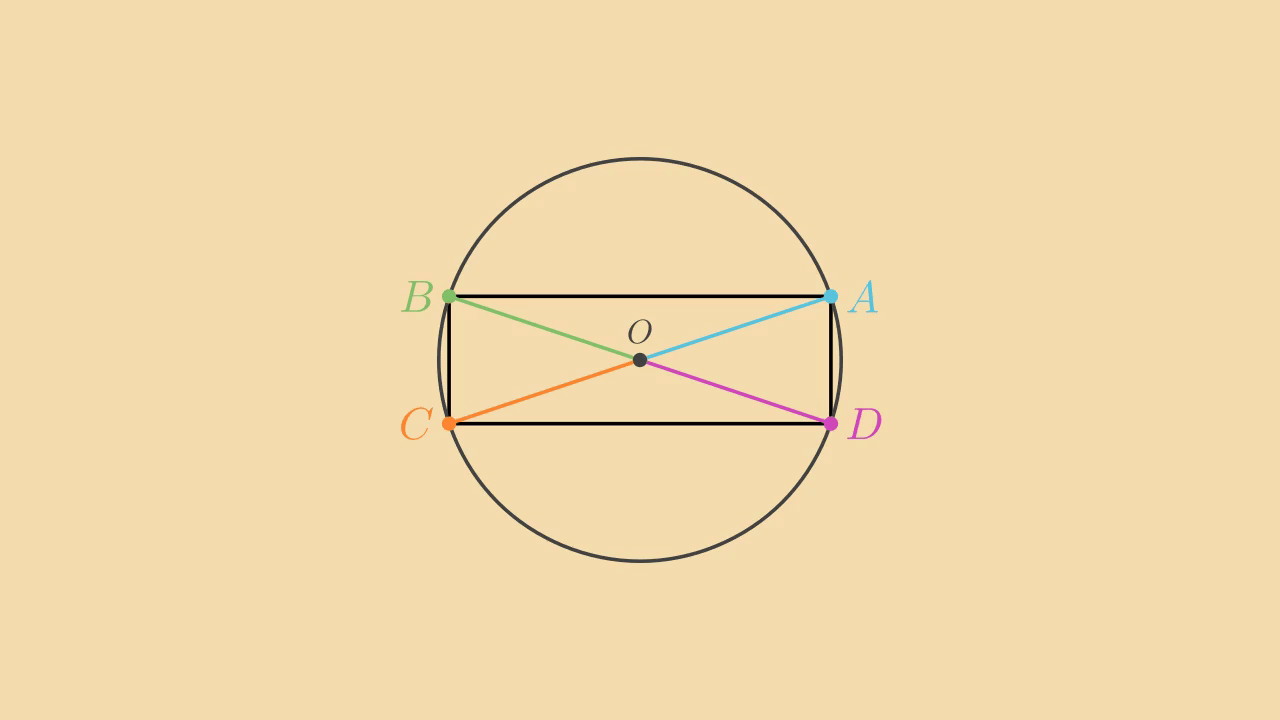
Figure 1 illustrates the situation. It's relatively straightforward to show that the corners are right angles. I'll show this for \(BCD\). We know \(B = -D\) so that the lines \(BO\) and \(OD\) are in the same direction through the origin. So, we know that \(\angle BCD\) and \(\angle COD\) must be complementary. But we also know that \(BCO\) and \(CDO\) are isoceles triangles, so the angles at the bases are equal, and we know that the internal angles add to \(\pi\), same as the angles \(\angle BOD\) and \(\angle COD\). So, we can conclude that \(\angle BOD = 2 \angle OCD\) and \(\angle COD = 2 \angle BCO\). But this implies that \(\angle BCO + \angle OCD = (1/2)(\angle BOD + \angle COD) = \pi/2\)... that is, that the corners are at right angles.

(There is probably a less numeric/more pure-geometry way to prove this that doesn't appeal to exact angle measures, but I don't care enough to find it.)

Anyway, let's see if we can construct an algebraic proof that \(B = -D\) and \(A = -C\).

My first thought is to use the angles, but exploring that a bit I don't think it works. You can use \(A + B = -C - D\) to show that the corresponding angles are sort-of-complementary, but I don't think that lets you separate out the two things.

Maybe it helps that the points are in clockwise order? It seems like it should be important somehow, anyway.

Maybe it is useful to rephrase what we are trying to do? We can restate this as saying we want to show that given \(A\) and \(B\) on the unit circle there is one and only one pair of unit circle numbers \(C, D\) so that \(A + B = -C - D\), namely \(C = -A\) and \(D = -B\).

I don't immediately see how this helps, so let's try a reminder? Suppose we rewrite \(A, B, C, D\) in terms of the corresponding angles \(0 \leq \alpha < \beta < \gamma < \delta < 2 \pi\) so that \(A, B, C, D\) correspond to \(e^{i\alpha}, e^{i\beta}, e^{i\gamma}, e^{i\delta}\). We want to show algebraically that \(C/A = -1\), \(B/D = -1\), or equivalently \(\gamma - \alpha = \pi\) and \(\delta - \beta = \pi\).

Clearly if we can show that \(A = -C\) then it follows that \(B = -D\), since \(B = -A -C - D = -(A + C) - D = -D\). So let's focus on that.

I think the key observation is that we can put a length-1 thing on the left side and that forces the right side to be length 1. I think we can use that to our advantage. To illustrate, suppose we use this rearrangement \(A = -B - D - C\). We know that the magnitude of \(A\) is 1, since it lies on the unit circle. But that implies that \(-B -D - C\) also has magnitude 1. But we know that each one of our complex numbers has magnitude 1, so this is not even greater than one magnitude. What we'd like to do is argue that some pieces must be canceling each other out.

The problem is how do we show this?

Here's one approach: Use the triangle inequality. We know that \(|B + D + C| = |C| = 1\). By the triangle inequality we also have \(|B + D + C| = 1 \leq |B + D| + |C| = |B + D| + 1\)... wait, damn, that doesn't work. I was hoping to get \(|B + D| \leq 0\) but clearly can't get there from here...

Hmm.

Okay, here's another angle. We can also write the square magnitude algebraically as \((B + C + D)(\overline{B + C + D} = 1\) and expand out to get:

\[B\bar{B} + B\bar{C} + B\bar{D} + C\bar{B} + C\bar{C} + C\bar{D} + D\bar{B} + D\bar{C} + D\bar{D} = 1\]

Then we can subtract out \(C \bar{C} = 1\)... but this looks like a mess. We can simplify it slightly by subbing in the other magnitudes:

\[2 + B\bar{A} + B\bar{C} + C\bar{A} + C\bar{B} + D\bar{B} + D\bar{C} = 0\]

But this is still pretty bad and not clearly moving us in the right direction.

Maybe it's useful to sub in the angular definitions here:

\[2 + e^{i(\beta - \delta)} + e^{i(\beta - \gamma)} + e^{i(\gamma - \delta)} + e^{i(\gamma - \beta)} + e^{i(\delta - \beta)} + e^{i(\delta - \gamma)} = 0\]

No, that doesn't seem better. But it gives me an idea. Clearly some of these terms are conjugates, should have noticed that earlier, and actually we can group them as twice the real part of (some product):

\[2 + 2\operatorname{Re}[B\bar{D}] + 2\operatorname{Re}[C\bar{B}] + 2\operatorname{Re}[C\bar{D}] = 0\]

I recall something from Visual Complex Analysis about \(z\bar{w}\): The real part is sort the dot product between the vectors, I think. So if \(z = a + bi\) and \(w = c + di\) then \(\operatorname{Re}[z\bar{w}] = ac + bd\).

I think what we might want to show here is that \(\operatorname{Re}[C \bar{B}] = -\operatorname{Re}[C\bar{D}]\). That would imply that \(\operatorname{Re}[B\bar{D}] = -1\) so that \(B = -D\).

How do we show that? Some other time.